Rethinking the FFT

By J. Greg Nash, Centar LLC, Los Angeles, California

Introduction

It is well known that the discrete Fourier transform (DFT) is of central importance to many signal processing applications, in particular high data-rate multicarrier applications such as wireless communications, which is the second largest market for semiconductor chips. Here a DFT is required in a large variety of wireless transmission protocols that are based on some form of orthogonal frequency division multiplexing (OFDM). What is unique about the wireless signal processing sub-domain is that the FFT circuitry used to calculate a DFT is being simultaneously stressed in a number of ways as the transmission protocols attempt keep pushing data rates up and latencies down in a mobile, crowded environment and at the same time improving quality of service while lowering cost and power consumption. Examples of the variety of requirements are:

• run-time choice of DFT sizes (scalable OFDM)
• larger transform sizes (LTE: 2K points; DVB: 32K points)
• high throughputs as a result of MIMO data streams and carrier aggregation (LTE Advanced 100MHz bandwidths)
• non-power-of-two DFTs (LTE single carrier FDMA: 35 transform sizes; Chinese Digital Media Broadcasting Terrestrial: 3780 points)

Finally, wireless protocols have been and always will be evolving [1] with different protocols used in different parts of the world.

While there have been a multitude of different FFT designs proposed to meet this large present and future spectrum of requirements, they have historically been based on two algorithm/architecture models and unique instantiations of these models are typically applied to each separate application. In contrast Centar has created a completely new algorithm/architecture model that can be programmed for each separate application, yet at the same time can also provide better throughputs and lower power. The remainder of this note is a quick summary of this new model and its FFT circuit characteristics.

Background

Most high performance 1-D FFT designs fall into one of two categories: either “pipelined” designs (Fig. 1), or serial “memory-based” designs (Fig. 2). The pipelined designs are typically obtained from different permutations of the “signal flow graph” by projecting them onto a linear pipelined array of memory/register and arithmetic hardware. The pipelined designs can be very computationally efficient, but lack programmability and must deal with stage-to-stage irregularities and the complex permutation networks, commutators and butterflies, which can ultimately limit clock speeds and add hardware.

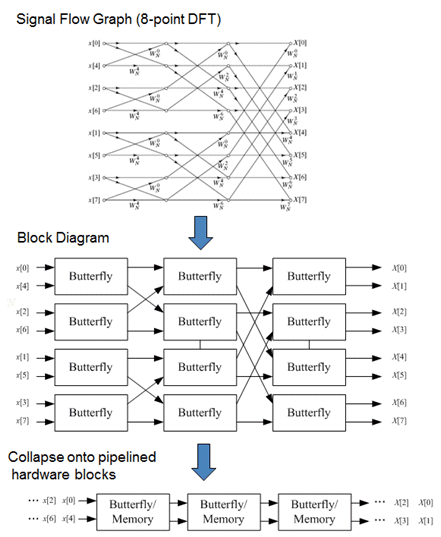
Fig. 1. Methodology for designing an 8-point pipelined FFT.

Memory-based designs consist of a plurality of large arithmetic units, where butterfly computations are performed, connected to a similar plurality of memories. The goal in such designs is to sequence data to/from the memories in such a way that available bandwidth is maximized.

Fig. 2. Traditional memory-based FFT architecture.

This design is more flexible because typically only a small number of butterfly units are used, so that by proper sequencing of data to/from the memories different functionality is possible. However, considerable complexity is usually required to achieve high speed either because many butterfly/memory units are required or because clock speeds must be very high. Additionally, the sequencing of data to from memories and butterfly units becomes very complex.

Centar FFT Model

Centar's design is also memory-based, but is architecturally very different than traditional memory-based approaches in that it is based on the fine grained array structure shown Fig. 3. It is seen to consist of many very small processing elements (PEs), each containing a multiplier/adder and a few registers with control logic. Each PE reads and writes to a typically small memory. Aggregate bandwidth is limited only by the number of PEs, e.g., no read/write conflicts can exist as in the memory-based model in Fig. 2.

Fig. 3. Centar array memory-based FFT architecture

Although not shown in Fig. 3, each PE is locally connected to its neighbors and data moves only between adjacent PEs. Input and output data flow into and out of the array from the top (not shown), using the nearest neighbor interconnection network.

Programmability

Here the concept of “programmability” is used loosely to mean that the same array circuit can be used to perform any set of transform sizes at the appropriate throughput rates. Additionally, other special functionality, as for example cyclic prefix insertion, which normally isn’t available in FFT IP, can easily be added. The benefit of a programmable circuit is that the computational hardware can be highly optimized and then reused with different control circuitry to do different classes of computations.

As long as a DFT of size N can be factored into powers of preferably small bases, a,b,c,…, e.g., N=anbmcp… , where n,m, and p are integers, programmability is achieved by performing appropriate sets of small DFTs. For example to do a 1024-point transform a factorization could be N=424142, resulting in 16*4 16-point DFTs followed by, 16*16 4-point transforms and finally 16*4 16-point transforms again. Since there are often many ways to factor a transform of size N, there are many potential orderings of small DFTs. The sequences of small DFTs are performed sequentially on the array in a way that all PEs are “active” almost all the time and thus the overall computation is very efficient.

Scalability

Scalability as used here is a measure of the throughput improvement (for a given FFT transform size) that can be obtained with a given amount additional circuit hardware. Ideally there should be a roughly linear relationship between the two. What’s unique about the memory model in Fig. 3 is that scalability is accomplished simply by duplicating the array or making it larger [2] or both, so that the computational structure remains the same and few design changes are needed. Alternatively, for the traditional pipelined FFT (Fig. 1) scaling is typically done by projecting the signal flow graph onto hardware that accepts more than the two samples per clock cycle as shown in Fig. 1; however, due to the irregularity of the signal flow graph there is no simple methodology for doing this and hardware typically grows faster than the throughput. For the memory based model in Fig. 2 there are inherent limits to scaling because of the difficulty in sequencing data to/from the memories in such a way that available bandwidth is maximized.

Example Design

As a basis for further discussion, two very common FFT (streaming) circuits were compiled using Altera’s software tools (Quartus II) with exactly the same settings (all synthesis options turned off) and the same target hardware (Stratix III EP3SE50F484C2 FPGA) [3]. The signal-to-quantization-noise (SQNR) results for the Altera circuits (IP v13.0) were obtained from a bit-accurate Matlab model created along with the circuit by the Altera FFT generators. Altera’s Timequest static timing analyzer was used to determine "worst case" maximum clock frequencies (Fmax) at 1.1V and 85C.

Table 1. Example 256 and 1024 point streaming FFTs

	Altera	Centar v1	Centar v2	Altera	Centar
	20 bits	16 bits	16 bits	20 bits	16 bits
Transform Size	256pts	1024pts
ALMs	4414	4024	5063	4770	4357
Memory (Kbits)	49	40.6	31.6	195	145
M9Ks	38	31	15	38	31
Multipliers (18-bits)	24	33	33	24	33
Fmax (data rate,MHz)	375	533	566	376	533
SQNR	76.6	86.7	86.7	81.3	82.9
µJ/FFT	1.29	1.12		6.36	4.31

Circuit comparisons shown in Table I are with Altera’s radix-4 delay-feedback 20-bit pipelined FFTs that use BFP (single exponent per FFT block) to achieve a similar SQNR as the Centar FFT circuits. Here the adaptive logic module (ALM) is the basic unit of a Stratix III FPGA (an 8-input "adaptive" LUT, two registers plus other logic). Fmax or clock rate is the same as the complex data sample rate.

Clock Speed (Fmax)

High FPGA clock speeds are obtained by minimizing logic levels and keeping interconnect distances short. Because the logic in the simple PEs in Fig.3 is primarily multiply-additions, which are performed in the embedded circuity, these are inherently fast. And because data movement is local, the interconnect delays for the critical path are less than the logic delays. Consequently, data rates >500MHz for the Stratix III 65nm technology are possible, whereas for most such FPGAs they are less than 400Mhz as seen in Table 1. This locality of data movement is particularly important as process technologies migrate to 22nm sizes and routing delays can become an increasingly dominant part of total the critical path.

Throughput

Throughputs are also enhanced because the algorithms used require fewer than the typical N cycles/DFT found in most pipelined streaming architectures. For example a 256 point transform can be performed in 165 clock cycles.

Power

Power dissipation is minimized by reducing LUT/register usage in the FPGA fabric and the nearest neighbor interconnection lengths are short, reducing capacitances. Here the Altera power per FFT (µ joules) is higher by 15/48% for the 256/1024 point transform sizes.

It should be noted that most of the FFT design literature focuses on minimizing the number of multipliers and memory blocks, which can be useful in an ASIC context; however, modern FPGAs have large numbers of embedded multipliers (as many as 868 on a single FPGA in the Altera Stratix III series) and embedded memories, which result in very different design tradeoffs compared to ASIC designs. And because multipliers and memories are embedded, their contribution to power dissipation is typically much less than the LUT/register fabric. For example in the 256/1024-point examples in Table 1, all the embedded components used only 14.4/14.7% of total power (minus I/O power).

SQNR

The dynamic range of an FFT circuit, which is usually characterized by the SQNR, is an important metric because of the tradeoff that exists between dynamic range and word lengths, e.g., longer word lengths are required for higher dynamic range. Centar uses both block floating point and floating point circuitry that’s an integral part of the design to provide higher SQNR values for a given fixed-point word length. For example in Table 1, the Altera streaming block floating point design needs at least 4 more bits to yield an equivalent SQNR. Other non-block floating point FFT designs would comparatively need more than 4 bits to maintain an SQNR equivalency.

Non power-of-two designs

The underlying DFT algorithms Centar uses also allow non-power-of-two transforms. A good example is the LTE single carrier uplink “LTE SC-FDMA” protocol that requires computation of 35 different non-power-of-two DFT transform sizes (12 to 1296 points) [3]. Centar’s circuit uses a single ROM memory to hold parameters that determine the specific factorizations and execution orderings used for loop index ranges in the verilog HDL coded control modules. (Any transform size or number of transforms can be performed by appropriate entries in this memory.) As can be seen in the normalized performance comparisons with other commercial circuits in Table 2 (average over 35 DFT sizes), this circuit is 2 to 3 times faster and the number of LUT/registers is relatively small (Table 3).

Table 2. Relative times to compute an LTE resource block for single carrier uplink DFTs (lower is better).

Design	Average Resource Block Compute Time
Centar	1.00
Xilinx [4]	2.14
Altera [5]	3.01

Table 3. FPGA resource fabric usage for uplink DFT circuitry

Design	FPGA	Registers	LUTs
Centar	Stratix III	3134	3582
Xilinx	Virtex-5	4743	4707
Altera	Stratix III	n.a.	2600

Conclusion

Centar’s goal is a single FFT algorithm/architecture with the programmability necessary to meet the variety of functional FFT demands of future wireless and other signal processing applications. Whereas traditionally such programmability must be traded off for performance and/or power dissipation, Centar’s array memory-based approach actually excels in providing both very high throughputs and low power.

References

[1] “5G Wireless Communication”, IEEE Communications Magazine, February 2014, Vol. 52, No.2.

[2] J. Greg Nash, Computationally efficient systolic architecture for computing the discrete Fourier transform, IEEE Trans Sig. Process., V. 53, Dec. 2005, pp. 4640-4651.

[3] J. Greg Nash, High-throughput programmable systolic array FFT architecture and FPGA Implementations, presented at the 2014 International Conference on Computing, Networking and Communications (ICNC), CNC Workshop (ICNC'14 - Workshops - CNC),Honolulu, HI, Feb 2014.

[4] Xilinx Discrete Fourier Transform v3.1, DS615 Mar. 1, 2011.

[5] Altera DFT/IDFT Reference Design, Application Note 464, May 2007.