The Importance of True Randomness in Cryptography

Introduction

In the world of information security, we often see statements such as ‘secured by 128-bit AES’ or ‘protected by 2048 bit authentication’. We are used to people asking about the strength of the cryptographic algorithms deployed in a security solution. Algorithms such as the AES, RSA and ECC have a proven track record of being difficult to break. They are successfully deployed in protocols that protect our identity and the integrity and confidentiality of our data, on a daily basis. Consider, for instance, the use of SSL or TLS when you buy a book at Amazon, or when you connect to your bank account to transfer a sum of money. Or the use of IKE and IPsec when you connect your laptop to the company network to check on your email and read documents stored on the company network. You can probably think of many other examples.

What we see very rarely, unfortunately, are statements about the strength of the random number generator used by a security system. System designers are typically more concerned with the power consumption and bit generation speed, than with the actual randomness of the bits generated.

This is strange, considering that in most, if not all, cryptographic systems, the quality of the random numbers used directly determines the security strength of the system. In other words, the quality of the random number generator directly influences how difficult it is to attack the system.

This can be easily seen if you realize that modern cryptographic algorithms and protocols are designed around a well-known principle by Kerckhoff, which roughly translates into the statement that

The security of the system must depend solely on the key material, and not on the design of the system.

This means that all modern security algorithms and protocols have their ‘cryptographic strength’ expressed in the number of (key) bits that an attacker needs to guess before he can break the system¹. This expression of strength implicitly assumes that the attacker has no knowledge of the bits of the original key used. The ‘effective strength’ of an algorithm is diminished when better attacks against it are found and more key bits can be derived from looking at (a limited amount) of output data.

Take, for example, the effective strength of 3DES. Although it uses 3 keys of 56 bits each, 3DES is currently only expected to provide 112 bits of ‘effective’ security, since the best attack against it today has a complexity of 2¹¹² bits. This still assumes that all 168 bits of the key used, are unknown and unpredictable by the attacker. So what happens if we start with key material that is partly predictable to the attacker? Immediately, the security of the system is weakened, regardless of the algorithm or protocol used. If your 128-bit key contains 16 predictable bits, using it in AES-128 doesn’t give you 128-bit protection; it only gives you 112 bits of protection, making the security of your system ‘only’ as strong as 3DES today.

And it doesn’t stop with cryptographic key material. Many security protocols require random bits to remain secure, even though the protocol definition will not always call it random; typically, a protocol description will use the term ‘unpredictable’ to indicate that a certain value should be difficult to guess by an attacker. True random numbers may be required if your application uses one of the following:

• keys and initialization values (IVs) for encryption
• keys for keyed MAC algorithms
• private keys for digital signature algorithms
• values to be used in entity authentication mechanisms
• values to be used in key establishment protocols
• PIN and password generation
• nonces

Exactly for the reasons mentioned above, the IETF has written a ‘Best Practices’ document (RFC 4086 (1)) to explain the importance of true randomness in cryptography, and to provide guidance on how to produce random numbers. NIST has a section on Random Number Generation in their Cryptographic Toolbox pages, and a number of standards bodies such as IETF, IEEE, NIST, ANSI, and ISO have, or are working on, standards related to random number generation. This goes to show the importance of proper random number generation.

Random Number Generation

Creating Random Numbers is hard. Especially if all you have available to do it, is digital hardware and deterministic software. Where is the randomness in that? Both are designed to behave predictably, each time, every time. Therefore, hardware and software designers, trying to find unpredictability, have to look outside of their normal operating environment to find it. Software typically uses external events (hard disk seek timing, keyboard/mouse clicks, Ethernet packet arrival intervals). Digital hardware designers have to ‘fall back’ to the analog world from which their digital environment normally tries to shield them. This typically means somehow translating the noise from a diode p-n junction, a resistor, or some other semiconductor component, into ‘unpredictable’ bit values.

But even if you have found a proper source of unpredictability, you’re not home free. There are still questions to ask, such as

• How much ‘unpredictability’ does my source generate ²
• How do I translate this unpredictability, into random bit streams or numbers?
• How efficient is this translation? Am I loosing unpredictability?
• Is the resulting data biased or not (for instance, does the data contain more zeroes than ones?)
• Do I get sufficient unpredictable output for my purpose?
• Are all the output bits I am getting, unpredictable, or only a portion?

Some organizations, such as NIST, have defined statistical tests to be run on the output of a random number generator to provide answers to some of the questions above (2). The challenge is, however, that statistical tests can’t really ‘prove’ that a source is random. At best, these tests can determine that a source is not, or only partially, unpredictable. As we will see below, it is very well possible to create a module that creates a bit string that will pass all the statistical tests available, but still generates a completely predictable bit stream, once you know the internal state of the module. For this reason, standardization- and certification organizations tend to require that a random number generator design is not tested by passing its output through a statistical test; rather, these organizations require that the design of the generator is reviewed, and its randomness generation properties explained and proven.

The general idea here is that True Random Number Generation is surprisingly difficult to do right. One of the results is that even now, there is no ‘approved’ or ‘standardized’ method for generating true random numbers. All that is available today are statistical tests (NIST, DIEHARD (3) etc) or evaluation criteria, such as the German AIS-31 specification ( (4), (5)).

Intrinsic Randomness versus external Noise

When selecting a source of randomness it is essential to understand whether the randomness of the source is caused by an integral property of the system itself, or if the source really is ‘just’ a measure of events external to, and unpredictable by, the system itself. The former is typically called ‘intrinsic’ randomness, the latter has different names but since the ‘signal’ in question is typically not part of the ‘desired’ operation of the system, in this whitepaper we shall refer to it as ‘external noise’. The difference is important, since, by definition, sources of intrinsic randomness cannot be influenced by an adversary, whereas sources using external noise can typically be influenced. In reality, of course the boundary between these types of sources is not as black and white as the definition suggests. Take, for instance, thermal noise as an example. Although this noise is present in all semiconductors, an adversary still has influence over it, by changing the temperature of the semiconductor. However since he does not have total control over it (unless he cools the system to 0K), thermal noise is still typically considered a source of intrinsic randomness.

Although sources of external randomness can be often be easily recognized (one can imagine an attacker influencing packet arrival rates, or keystroke timing), they may often not be too easily disregarded. In the case of thermal noise above, for instance, an application wishing to extract unpredictable bits by sampling the noise current or voltage, also has to deal with the presence of voltage noise on the power lines, which, although it is considered noise, is predictable and, more importantly, controllable by an adversary. Thus, the sampling process must ensure that the intrinsic randomness is not ‘drowned’ by the external noise.

The conclusion with respect to random number generators is that in most systems, it is desirable that the RNG uses (or is characterized by) purely intrinsic sources of randomness, but that unfortunately this cannot always be guaranteed.

Deterministic Randomness?

In literature, two classes of random number (or bit) generators are identified: the Non- Deterministic (or True) Random Number Generators, and the Deterministic (or Pseudo) Random Number Generators. The two types differ by the fact that a TRNG³ uses some source of randomness to generate its output, whereas a PRNG does not – the output of a PRNG is therefore completely predictable (or deterministic) once its internal state is known. If this is the case, then why are PRNGs still so important? Some of the reasons are

• As long as a PRNG’s internal state is unknown to an attacker, the output it generates is unpredictable by the attacker – the same quality we need from the output of our TRNG. PRNGs are much easier to construct in digital hardware than a TRNG.
• A well-constructed PRNG only leaks a limited amount of data about its internal state through the output it produces. So as long as the PRNG’s internal state is refreshed by new unpredictable data (the PRNG is ‘reseeded’) often enough, its output remains unpredictable. Thus, you can generate a lot of unpredictable data from a limited amount of truly random data – as long as you keep your internal PRNG state secret.
• Once a PRNG is properly seeded, it can generate unpredictable output very fast – a useful property for systems that need a lot of unpredictable data in a short amount of time. Collecting random bits from a source of randomness typically is a difficult, and slow, process.

We shall see that many of the assurance requirements on random number generators are based around the protection of this internal state.

In many cases, a random bit generator is constructed from a combination of a source of true randomness, which is used to seed the internal state of a PRNG. These types of random number generators are called ‘Hybrid’ RNGs.

Bias

Most sources of random data generate ‘biased’ output, i.e. the chance that an output bit is ‘1’ or ‘0’ is not equal to 0.5. In other words, the source generates more ‘1’s than ‘0’s, or vice versa. If this is the case, the output of the random data source must be post-processed such that the output bits after post-processing have an equal chance of being ‘1’ or ‘0’. This post-processing is often called ‘whitening’ after the term in image noise processing, which transforms the frequency spectrum of some random variable into a flat spectrum with equal power in all frequencies (thus, ‘white’ light). In the context of random number generators, ‘whitening’ means transforming the output of the random data source, to a bit stream with a zero mean and ‘normal’ distribution. The whitening function is typically combined with the PRNG function, for instance by the ‘Hybrid’ RNGs discussed above.

Randomness Assurance

Several standards bodies (national and international) have created requirements and recommendations for the construction, testing and use of random number generators, in order to seek assurance that the output they produce is indeed random. Some of the more well-known specifications, and their impact on TRNG design, are briefly described, below.

FIPS 140-2, -3 (draft), and NIST SP 800-90

The current version of the NIST Security Requirements for Cryptographic Modules (FIPS 140-2, (6)) contains the following entries related to random number generation:

• The Data Output from the RNG use (and pass) the continuous random number generator tests (see below).
• The approved algorithms used by the RNG and/or its postprocessor shall be tested using known answer tests at power-up.
• The requirement for the RNG to pass a number of statistical tests for ‘randomness’ (monobit test, poker test, runs test, and long runs test) have been removed from the FIPS 140-2 specification by change notice 2, December 2002.
• Annex C of FIPS 140-2 lists the approved Deterministic Random Number Generators; this list has been replaced completely (see FIPS 140-3 below). Notably, a popular 3DES-based postprocessor specified by ANSI X9.31 was on the list but will no longer be approved by FIPS 140-3.

NIST is currently working on the successor of FIPS 140-2. The current draft version, to become FIPS 140-3 (7), has seen a few iterations with different levels of requirements on deterministic- and non-deterministic random number generators. Most notably, the current draft of FIPS 140-3.

• No longer refers to ‘Random Number Generators’ or RNG’s, but now uses the terms ‘Deterministic’ (or Non-Deterministic) Random Bit Generator, DRBG and NDRBG, respectively.
• Specific references to randomness- and other statistical tests on the output of the RBG have been removed (following the change note on FIPS 140-2 already mentioned).
• Focuses on making sure that RBGs are constructed correctly, and
• Adds requirements to model the entropy generation rate of the entropy source, if used.

The last version of the draft available at the time of the creation of this whitepaper (FIPS 140-3 Revised Draft Nov. 9, 2009), contains the following statements with respect to random bit generators (deterministic and non-deterministic), focusing on assurance that the design is still functioning as intended, and that the RBG is constructed properly:

• The internal state of a DRBG shall be considered a Critical Security Parameter (thus, it must be protected and remain confidential).
• Depending on the assurance level, there are different requirements on when to reinitialize the seed of the RBG. Similar statements exist on zeroizing the RBG state.
• All RBGs used in a design shall be documented and shall be one of the approved or allowed types of RBG (see below).
• All security parameters in the system that require a random value, shall create such a value using an approved (or allowed) RBG.
• The entropy generation method and the (claimed) minimum entropy generated by the source, shall be documented.

In most cases, the last bullet is the hardest to comply with.

The FIPS 140 requirements still specify a number of known-answer self tests for security-critical functions; these include the operation of the approved algorithms used by the RBG circuit and the post-processing logic.

FIPS 140 refers to another NIST Special Publication, SP 800-90 (8), for the list of approved and allowed RBGs. It is good to note that

• SP 800-90 relates only to deterministic RBGs. So currently, there is no ‘Approved’ NDRBG (no standard method for true random number generation exists).
• Similar to the FIPS 140 document, Appendix C of SP 800-90 requires that the developer provides a model to justify his claims on the entropy generated by the entropy source.
• Appendix D of SP 800-90 shows how an ‘Allowed’ NDRBG can be built from an entropy source and an Approved DRBG.

In conjunction with FIPS 140 and NIST SP 800-90, NIST also maintains a suite of statistical tests to verify the randomness of the output of an RBG; this publication, NIST SP 800-22, was updated recently to SP 800-22rev1a (9).

ISO 18031: Information Technology - Security Techniques - Random Bit Generation

ISO 18031 (10)is somewhat comparable to FIPS SP 800-90, with the exception that ISO 18031 specifically targets non-deterministic bit generators and provides requirements for them. Unlike the NIST publications, the ISO specifications are copyrighted so it’s not possible to go into too much detail; sufficient to say here that like the FIPS specifications, ISO 18031 requires health checks on the design and a model for the prediction of the amount of entropy generated. The construction of NDRBG’s by combining a source of entropy with a DRBG is also similar to FIPS SP 800-90. Contrary to FIPS though, ISO 18031 does require continuous statistical tests on the output of the RBG.

ANSI X9.82

The ANSI X9.82 (11) specification comprises 4 parts, of which 2 parts:

• Part 1, the introduction and overview
• Part 3 (the part on deterministic RNGs) are available from ANSI.

Part 2 (Entropy Sources) and Part 4 (RBG constructs) are still in draft (Working Group X9F1).

German BSI AIS-20 and AIS-31

The German BSI, the Bundesamt für Sicherheit in der Informationstechnik, (the Federal Office for Information Security) has specified two ‘Application notes and Interpretation of the Scheme’ for use in the evaluation (for Common Criteria or ITSEC) of DRBGs (AIS-20, (12)) and NDRBGs (AIS-31). These documents contain a number of requirements on the CC criteria that need to be complied to, as well as a number of continuous- and startup tests that the design itself needs to employ, for a (N)DRBG to pass the evaluation.

AIS-20 targets deterministic RBGs. AIS-31 targets non-deterministic RBGs in particular. In AIS-31, two assurance classes of NDRBG are recognized. Class P1, aims to provide assurance that an NDRBG output ‘behaves well’ under statistical analysis. Class P2 adds requirements to provide assurance that the NRBG not only behaves well statistically, but is also resistant against systematic attempts to guess its output. Next to these two classes, AIS-31 also recognizes several levels of assurance (strength of mechanisms) to allow (for instance) validation under the different EAL levels recognized by CC.

A number of the prescribed tests concur (or are even taken from) the old FIPS 140 tests, however the requirements set by AIS-31 go quite a lot further, including a set of statistical tests that need to be run on the output of the TRNG, that is comparable to NIST’s SP 800-22 (see below), though with different pass/fail conditions. Some of the tests must be implemented in hardware directly, because they need to be executed continuously; other tests require the output of the NDRBG to be processed mathematically and thus require software support. A number of the tests listed by AIS-31 are only required ‘at evaluation time’ though the details depend on the desired evaluation level.

Like the other specifications, AIS-31 requires the developer to explain the underlying entropy source and the claimed entropy generation rates.

AuthenTec’s True Random Number Generator

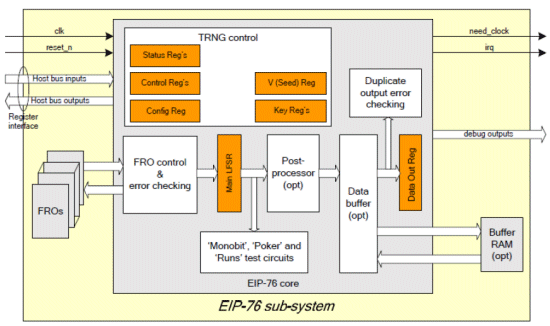
MOSFET Channel Noise as Source of Randomness

The AuthenTec SafeXcel-IP-76 True Random Number generator uses the current noise, present in the channel of a MOSFET transistor, as its source of intrinsic randomness. This noise causes a small amount of uncertainty on the transition time of an inverter cell when it switches from low- to high. This uncertainty is accumulated by placing an odd number of inverters in a ring, creating what is called a Free Running Oscillator (FRO). The uncertainty on the individual inverter transitions causes a small amount of phase jitter on the output of the FRO, which builds up over time, until at some point in time it can no longer be predicted if a certain point in the FRO ring has the value ‘0’ or ‘1’. By sampling the output of the FRO at such a point in time, the state of the captured bit cannot be predicted and thus, we have created a single bit of randomness.

The sampled bits are subsequently passed through an LFSR for initial whitening, after which they are subjected to numerous tests to verify that the output of the LFSR is indeed unpredictable (or at least, cannot be easily predicted because something has broken). Optionally, the output of the LFSR can be post-processed by a PRNG for further whitening and expansion, for instance if more unpredictable data is required than the entropy collection circuitry can provide. The AuthenTec TRNG uses the FIPS 140-3 approved ‘CTR_DRBG’ with AES-256 as post processor.

FIPS compliance

When discussing TRNGs (or more appropriately, NDRBGs but the acronym TRNG reads easier) we often get asked the question what is needed to ‘be FIPS compliant’. As stated earlier, NIST doesn’t currently provide guidance on ‘approved’ TRNGs, however when a system requires a TRNG, there are ‘allowed’ constructions, plus a number of requirements to be followed; roughly speaking

• The TRNG needs to use an approved post processor. The AuthenTec TRNG solution implements the SP 800-90 CTR_DBRG (required for FIPS 140-3, allowed for FIPS 140- 2).
• The TRNG’s entropy source must be explained and a model must be provided for its entropy generation rate (available from AuthenTec under NDA).
• The internal state of the TRNG (in particular, the post processor) must be protected. This is a system level constraint, similar to the requirement that the key material generated from the output of the TRNG must be protected. The AuthenTec TRNG solution provides an internal re-seed function where the random data used for the re-seeding is not revealed outside the module boundary.
• Various operational health checks should be present or supported. This is actually a requirement from SP 800-90 which is implied by FIPS 140. The AuthenTec TRNG solution (SafeXcel-IP-76) specifically implements the ‘continuous’ tests that cannot be triggered or executed by software. The SafeXcel-IP-76 supports this by providing state zeroisation functionality.

In addition, the TRNG employs patented circuitry to detect frequency locking of the free running oscillators, including a mechanism to break to lock and generate an alarm if locking occurs too often. Detecting if a FRO is locked to a system frequency is important since this can cause the accumulation of jitter on the frequency of the ring to be reduced or even negated completely, to a point where the sampling mechanism only samples a constant bit value or a recurring pattern of values. If multiple FRO rings show locking in this way, the TRNG is automatically stopped and further output is disabled. This test can be considered an ‘entropy source breakdown’ detection mechanism as required by AIS-31.

Integration in modern SoCs

When using a TRNG in your design, there are a number of things to consider (in addition to the topics from the previous sections). For instance:

• How many random bits does your application need per time unit?
• How much ‘randomness’ is needed in your application? Does it need to be fully random every time, or is it sufficient to occasionally re-seed the PRNG and create unpredictable data from there?
• How much power can the TRNG consume? More entropy gathering requires more FROs running simultaneously, so there is a relationship between entropy generation rate and power consumption.
• What frequency (range) to use for the individual FROs? Higher frequencies make it easier to collect entropy faster – but run a FRO too fast and there’s a risk it stops running at all. Similarly, you want to avoid running FROs at frequencies that are ‘multiples’ of any of the other (clock) frequencies in the design. In smaller technologies, however, the PVT range is typically so large that this constraint cannot be easily met over the complete range. In this case, the only remedy is to use more FRO’s – so even if some of them lock some of the time, there is still enough entropy generated by the others.
• Is the TRNG (scan) testable? By design, a TRNG contains constructs that violates typical design constraints, especially those for testability. A TRNG should provide a mechanism to allow it to be included in the regular scan test, regardless of all the health tests mentioned above.
• What SoC bus interfaces are available?
• Is software integration available?

AuthenTec took all of the above considerations into account when designing the latest state of the art version of the SafeXcel-IP-76 True Random Number Generator core family. The SafeXcel-IP-76 TRNG core family is provided with integrated AXI, AHB, PLB, or any other system bus interface and comes with Driver’s Developer’s Kit (DDK) to facilitate software development and easy porting to other platforms.

Licensing semiconductor IP from AuthenTec (Formerly SafeNet Embedded Security Division), the world's largest provider of silicon-proven security IP, makes it easy and cost-effective for chip designers to integrate the most advanced security functionality into semiconductor designs, including NPUs, communications processors, and custom ASICs and FPGAs. AuthenTec provides high-performance, highly integrated security engines that support cryptographic algorithms and protocol-related security operations for a wide range of applications. Silicon-proven and ready-touse, the SafeXcel IP security engines are a reliable security solution for chip designers - delivering quick time-to-market while reducing design and engineering cost. AuthenTec OEM products also include security stack software and security processors. This complete HW/SW security platform enables vendors to build integrated networking security solutions while reducing total cost and time to market.

About AuthenTec

AuthenTec is the world’s #1 provider of fingerprint sensors, identity management software, and embedded security solutions. AuthenTec security and identity management solutions address enterprise, consumer and government applications for a growing base of top tier global customers. Already shipped on hundreds of millions of devices, the Company's smart sensor products, software and embedded security solutions are used virtually everywhere, from the PC on your desk to the mobile device in your hand to the server in the cloud. AuthenTec offers developers and users secure and convenient ways to manage today's rapidly evolving digital identities and security needs. For more information, visit http://www.authentec.com or follow us at http://twitter.com/authentecnews.

References

1. Eastlake, D., Schiller, J. and Crocker, S. RFC 4086. RFC Editor. [Online] http://www.ietf.org/rfc/rfc4086.txt

2. Rukhin, A., et al. NIST Special Publication 800-22rev1a: A Statistical Test Suite for Random and Pseudorandom Number Generators. Computer Security Resource Center. [Online] http://csrc.nist.gov/groups/ST/toolkit/rng/documents/SP800-22rev1a.pdf 

3. The Marsaglia Random Number CDROM including the Diehard Battery of Tests of Randomness. [Online] http://www.stat.fsu.edu/pub/diehard/ 

4. Bundersamt für Sicherheit in der Informationstechnik. AIS-31. Functionality classes and evaluation methodology for physical random number generators. Andwendungen und Interpretationen (AIS) zu CC. [Online] https://www.bsi.bund.de/cln_165/ContentBSI/Themen/ZertifizierungundAnerkennung/ZertifierungnachCCundITSEC/AnwendungshinweiseundInterpretationen/AISCC/ais_cc.html  

5. Killmann, W. and Schindler, W. Dr. A Proposal For: Functionality classes and evaluation methodology for true (physical) random number generators. [Online] https://www.bsi.bund.de/SharedDocs/Downloads/DE/BSI/Zertifizierung/Interpretationen/trngk31e_pdf.pdf.

6. FIPS PUB 140-2 Security Requirements for Cryptographic Modules. Computer Security Division: Computer Security Division. [Online] http://csrc.nist.gov/groups/STM/cmvp/standards.html#02 

7. FIPS 140-3 Draft. Draft Security Requirements for Cryptographic Modules (Revised Draft). Computer Security Division: Computer Security Resource Center: Publications. [Online] http://csrc.nist.gov/publications/PubsDrafts.html 

8. NIST SP 800-90. Recommendation for Random Number Generation Using Deterministic Random Bit Generators. Computer Security Division: Computer Security Resource Center: Special Publications (800 Series. [Online] http://csrc.nist.gov/publications/PubsSPs.html

9. SP 800-22rev1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Computer Security Division: Computer Security Resource Center: Special Publications (800 Series). [Online] http://csrc.nist.gov/publications/PubsSPs.html 

10. ISO. ISO/IEC 18031:2005. ISO Standards. [Online] http://www.iso.org/iso/catalogue_detail.htm?csnumber=30816 .

11. ANSI. ANSI X9.28:2006. ANSI Standards Store. [Online] http://webstore.ansi.org/RecordDetail.aspx?sku=ANSI+X9.82-1%3A2006 

12. Bundersamt für Sicherheit in der Informationstechnik. AIS-20. Functionality classes and evaluation methodology for deterministic random number generators. Anwendungshinweise und Interpretationen (AIS) zu CC. [Online] https://www.bsi.bund.de/cln_165/ContentBSI/Themen/ZertifizierungundAnerkennung/ZertifierungnachCCundITSEC/AnwendungshinweiseundInterpretationen/AISCC/ais_cc.html .

For more information, visit www.authentec.com/embedded  

AuthenTec Embedded Security Solutions

December 14, 2010

¹ The actual definition of cryptographic strength is a measure of the complexity of a computational attack against the algorithm, often expressed as the 2log of the number of times attacker must invoke the algorithm before learning the value of the key used

² ‘Unpredictability’ is often expressed as ‘entropy’ which is a measure for the uncertainty associated with a random variable. Note that entropy is used here as defined for the context of information theory. Entropy is used in many different places with different definitions, such as in thermodynamics or statistics

³ Note that NIST, and others, also use the terms deterministic and non-deterministic ‘random bit generator’ or DRBG and NDRBG, to indicate basically the same two classes of randomness generators, though the NIST versions are assumed to output only ‘ones’ and ‘zeroes’.