By Julian Jenkins, Perceptia Devices
1. Introduction
No real clock sources (PLL’s, DLL’s, Crystal Oscillators, even function generators) exist that have a single, fixed value for their output period. The output period of all real clock sources changes over time. The exact placement of clock edges will vary both within a clock period and from one clock period to the next. This variance in period is known as jitter.
This article explains a some of the key terminology and parameters commonly used to describe jitter. It will also help clarify the most important parameters for a some PLL applications, allowing the designer to better understand what is required from a PLL.
This article is part of a series on specifying jitter for PLLs. The next article in this series will consider jitter in the context of clocked logic. It will discuss the relationship between timing closure and jitter and how to determine the correct timing constraints from the jitter specifications of a PLL.
The final article in this series will consider the use of PLLs in RF systems and for clocking ADCs and DACs. It will discuss the relationship between SNR and jitter and how to determine the jitter requirements for a PLL used in such a system.
2. Applications
Different applications have different requirements for jitter. This document discusses the major system archetypes and how they each require different analysis methods and use different methods to account for jitter when resolving jitter budgets. In particular the important requirements pertaining to PLL performance and jitter specifications are addressed.
2.1. Digital Systems
In a digital system, the clock defines a period of time during which the circuits can achieve a certain amount of work. Since each sub-unit of work (logic gate intrinsic delay, rise/fall transition delay, wire delay etc) takes a certain period of time to complete, then the overall frequency (period) of the system is a major constraint on logic complexity and allowed logic depth in synchronous digital systems.
The period of the clock, sets the time available for the unit of work to complete. This is related to the frequency by the following equation:
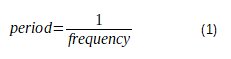
In digital systems, clock edges define the time at which each work unit starts and ends. When jitter changes edge timing to reduce the length of an individual clock cycle it reduces the amount of time available for the unit of work to complete.
Period jitter (see Section 4.2) is a measure of how individual clock cycles vary and hence is the best indicator of how much time is available for each unit of work. This is the primary characteristic that digital systems designers should focus on and closely specify.
2.2. RF Systems
The Local Oscillator (LO) for an RF system defines the carrier frequency and is generally used in the mixers used to generate the transmitted signal and down-convert the received signal for processing.
In this context, accumulated jitter (see Section 4.4) is a measure of the total phase noise in the system. When a signal is multiplied by a clock to up-convert or down convert, the resulting spectrum becomes the multiplication of the spectrum of the signal with the spectrum of the clock. Any phase noise in the clock signal will result in an undesired signal at the output, reducing the signal to noise ratio (SNR) of the system.
The power in the unwanted part of the output signal due to phase noise is proportional to the jitter. The mathematics for calculation of the SNR as a result of jitter are well understood.
Accumulated jitter is the phase noise integrated across the bandwidth of a channel. Only jitter within the channel bandwidth will affect the system, everything outside this will be filtered.
2.3. ADCs and DACs
In Analog to Digital Converters (ADC) and Digital to Analog Converters (DAC), the clock sets the time at which the sample is taken. If the signal is changing with time and jitter causes the sampling time to change from the ideal instant, this will result in a change in the sampled value of the signal versus an ideal reference sample value.
The sampling of an ADC or DAC can be modeled as a multiplication of the signal with the clock. This means that the SNR of such a system is degraded in exactly the same was as described in Section 2.2 and accumulated jitter is again the important parameter.
2.4. Serial Communications
When transmitting or receiving a serial bit stream, using a SerDes or similar, the clock is used to encode and time the transmitted data, embedding clock information within the transmitted data itself. Separately the receiver has it’s own clock, derived from the received data, to sample and capture the data. In this system, accumulated jitter is important as this sets the difference in time between when a bit arrives and when that bit is sampled. If the jitter of this combined system is too big, then the wrong bit value will be sampled.
Only high frequency accumulated jitter is important for serial communications except in special cases. This is because a SerDes typically includes a clock and data recovery (CDR) subsystem that determines the best time to sample the data from the data itself, which as noted previously has transmit clock information embedded within it. This CDR will be able to track low frequency jitter, sometimes referred to as wander in this context, however high frequency jitter will be outside the bandwidth of the CDR and cannot be tracked out.
3. Random and Deterministic Jitter
When measuring jitter, it is important to consider the behaviour across many cycles to see what the aggregate performance will be in a statistical sense. For RF Systems, ADCs and DACs, this statistical data generates the important information that the system designer needs directly whilst for digital systems, it gives the probability that a clock cycle will be shorter than the target cycle time, which is the key metric for timing closure.
3.1.1. Random Jitter (RJ)
The jitter generated within a PLL is primarily band limited random jitter. In addition white noise on the PLL supplies can be translated into random jitter at the PLL output.
Random jitter comes from processes that are truly random such as thermal noise and flicker noise. Random jitter may also result from power supply noise, where that noise in turn originates from random processes, such as thermal noise, in the circuit supplying power to the SoC, and in particular to the PLL.
Random jitter, as its name suggests, cannot be predicted accurately for any given cycle. Only the statistical properties of a set of clock cycles can be estimated. The most useful measure of RJ is the standard deviation of the random distribution, which is the same as the RMS jitter.
In a true random distribution following a normal distribution, each sample is totally independent of each other sample, so it is possible to have the maximum possible value immediately followed by the minimum possible value. However this is the same as an infinite bandwidth white noise signal and, in practice, all electronic systems have limited bandwidth. Further, the circuits used in all PLLs, result in phase noise characteristics that have the great majority of their power at low modulation frequencies. This results in band limited random jitter, which is a good match for a normal distribution, but has reduced probabilities of events occurring that are a large number of standard deviations from the mean.
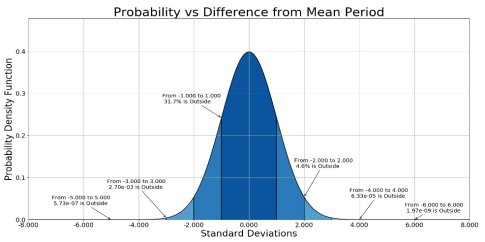
Figure 1: The Normal Distribution
Figure 1 shows the normal distribution, typically used to model jitter probability. All random jitter from a PLL follows a normal distribution.
When specifying a system, we must choose an acceptable probability (confidence interval) that the instantaneous jitter of a particular clock edge may be greater than a given acceptable value of peak jitter (See Section 5).
For each whole standard deviation (σ) from 1 to 6, the probability of a clock edge being outside that number of σ from the mean is annotated on Figure 1. It can be seen that this approaches zero very quickly, but never reaches zero. For example, there is a 31.7% chance that a clock edge is more than 1σ from the mean, but the probability that is more than 6σ from the mean is 1.97 × 10-9, a number so small that in almost all analysis cases we can approximate it to zero.
For example, JESD65B specifies that the period jitter should be measured over 10000 samples. This corresponds roughly to a probability of 1:10000 of having a period shorter than the shortest measured and, referring to the graph of figure 1, we must expect the the peak period jitter resulting from such a measurement to be at least 4σ. Students of probability will understand that the peak period jitter will be different for each sample of 10000 clocks measured, but that this is sufficient samples to give a good estimate of σ.
Note that modern digital designs often use more stringent criteria than this, requiring a confidence interval of 5σ or even 6σ. Serial communication standards commonly have even higher requirements and typically specify a larger number of σ that must be used to calculate the peak jitter.
If there are multiple sources of uncorrelated random jitter, they are summed in an RMS fashion. Thus to get the combined σ:
![]()
Where:
-
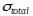 is the total jitter
is the total jitter -
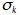 for k = 1...n, are the individual, uncorrelated jitter components.
for k = 1...n, are the individual, uncorrelated jitter components.
Note that correlated random jitter components add linearly.
3.1.2. Deterministic Jitter (DJ)
Deterministic jitter is jitter that follows a known pattern.
Potential sources of deterministic jitter in clock outputs are:
-
Spread spectrum clocking (SSC)
-
Deterministic modulation of the power supply
-
e.g. If an SoC has repeating high power and low power modes, this can result in deterministic power supply modulation.
-
-
Other sources of modulation
-
Any other mechanism that operates in a deterministic manner
In data transmission systems, data dependent jitter (DDJ) is a deterministic jitter component that depends on the prior data symbols that have been transmitted. Clock signals are equivalent to a repeating 0101 pattern and have no DDJ since the data pattern is invariant.
The peak deterministic jitter can be measured directly. Because it is deterministic and has no probabilistic dependancies, the measurement is absolute. However, random jitter will always be present in any system and it’s contribution to the measurement must be taken into account.
For example the voltage supply to a PLL may exhibit a 500kHz ripple arising from the use of a switched mode power supply. This power supply noise component will result in deterministic period jitter at the PLL output with a measurable peak value which will be proportional to the peak deviation of the input supply. There will be a direct relationship between the power supply voltage at a given time and the instantaneous period jitter of the PLL output clock. As the power supply voltage changes the change in period at the PLL output will be seen as deterministic jitter.
Deterministic jitter components, including DDJ, add linearly.
3.1.3. Combining Random and Deterministic Jitter
Only the peak or peak-to-peak values of random and deterministic jitter can be combined. To combine these two components:
- Take the peak value of the random jitter for a given sigma (Rj)Take the peak value of the deterministic jitter()
- Add the two peak values to calculate total jitter(Tj).
Tj = Rj + Dj (3)
4. Jitter Definition and Categories
4.1. Phase Noise and Spurious Tones
Phase noise is an alternate means to characterize the same underlying mechanisms and effects that are characterized by jitter. Phase noise measures the power spectral density (PSD) of the output clock. In some applications, specific characteristics of the phase noise spectrum are important and cannot be captured with a simple jitter number.
Spurious tones, often referred to as spurs, are specific output frequencies (other than the clock frequency) present in the clock signal. These are generally related to deterministic jitter. Note that the natural harmonics of the clock frequency generally change the shape of the output clock but do not contribute to jitter.
In many RF systems, the specific properties of the phase noise are important. In these cases, accumulated jitter may be a convenient aid in the calculation or analysis for budgeting purposes, but it should not be used for final system characterization.
All forms of random jitter can be calculated from the phase noise of a signal by applying appropriate filtering/windowing and integrating the result. This allows most users to have a convenient measure of the jitter of a signal without requiring detailed knowledge of the complete PSD of the signal. Note that in RF systems, ADCs and DACs, increasing phase noise/jitter results in reduced SNR.
Most forms of deterministic jitter can be calculated from the spurs present in the spectrum of the output clock, making the PSD a highly useful jitter parameter.
4.2. Period Jitter
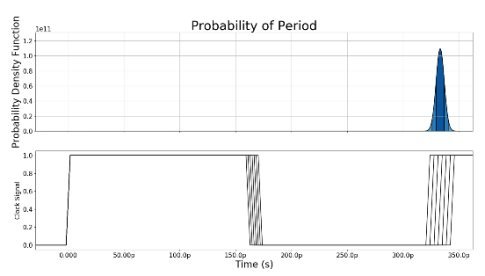
Figure 2: Period Jitter Definition
Period jitter is the most important jitter for digital systems. It is the deviation in the period of the clock from the mean period of that clock.
Figure 2 shows an example of period jitter for a 3GHz clock. Each cycle plotted on the lower axis has a slightly different period from all the others, as shown by the several possible rising edge positions at the end of the cycle. All the rising edges at the beginning of the cycle have been aligned to show the differences in period arising from jitter. There will be some probabilistic distribution of the time of an edge happening, shown here on the upper axis as a normal distribution.
A plot similar to Figure 2 can be generated using an oscilloscope, triggered on the first rising edge. However, any real oscilloscope will add jitter due to noise arising from its internal sampling and triggering circuitry.
Mathematically, period jitter can be represented as:
jperiod = period current cycle - period mean (4)
Where:
- jperiod is the instantaneous period jitter of a given clock cycle
- period current cycle is the instantaneous period the current clock cycle
- period mean is the mean period of the clock being measured
Period jitter consists of both random and deterministic jitter components. These can be analysed individually, but it is generally unimportant to do so because in most applications where period jitter is important the only important parameter is the shortest possible cycle.
In a digital system, is the time available for the logic to complete its unit of work.
4.3. Cycle-to-Cycle Jitter
Cycle-to-cycle jitter measures the change between two adjacent clock cycles. This is shown in Figure 3.
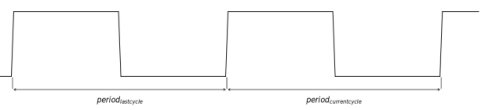
Figure 3: Cycle-to-Cycle Jitter Definition
Mathematically, cycle-to-cycle jitter can be represented as:
jcc = period current cycle - period last cycle (5)
Where:
- j cc is the instantaneous period jitter of a given clock cycle
- period current cycle is the instantaneous period the current clock cycle
- period last cycle is the instantaneous period of the last clock cycle
While commonly discussed in many treatments of jitter, cycle-to-cycle jitter is not generally useful as it does not relate to any commonly used performance criteria in digital, RF or sampled systems.
4.4. Accumulated Jitter
Accumulated jitter, also known as long term jitter, is the deviation in the time of a given clock edge from when the same edge of an ideal clock occurs. This can be accumulated over many clock cycles, as distinct from period jitter which only considers a single clock cycle or cycle-to-cycle jitter which is always measured for two clock cycles adjacent in time.
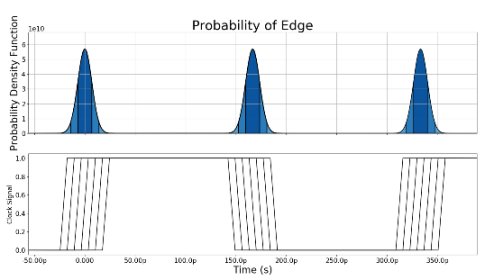
Figure 4: Accumulated Jitter Definition
Figure 4 shows a clock signal illustrating the concept of accumulated jitter. Without specifying a reference edge, the timing of the measured clock is considered. Each individual edge will have an uncertainty associated with it, this is the accumulated jitter.
A picture similar, to Figure 4 can be generated on an oscilloscope triggered on an edge long before the displayed edges (a reference edge). As the distance to the reference edge increases, the displayed jitter will increase until it reaches an approximation the total accumulated jitter value. Figure 4 is an example of this once the reference clock is sufficiently far away that the jitter has reached its accumulated value. However, the value shown on the oscilloscope will include the accumulated jitter of the internal sampling clock and the uncertainty of the oscilloscope’s triggering circuit which can add significantly to the measured value. Care should be taken to consider the accuracy and limitations of the oscilliscope or other measurement equipment when measuring any clock source. The jitter of high performance RF PLL’s like Perceptia’s pPLL08 will be below the noise floor of even the highest performance oscilloscopes and can only be measured in the frequency domain.
Accumulated jitter is larger than the period jitter, as it the the accumulation of the period jitter over many cycles. In real systems, we only need to consider the jitter over specific bandwidths, so the accumulated jitter will reach a limit independent of time and will not become infinitely large.
Accumulated jitter is important for serial communication, RF systems and for the clocks to ADCs and DACs. Accumulated jitter is the sum of both random and deterministic components.
Accumulated jitter is integrated over a frequency band that matches the application. For example, in an RF system, the integration band may match the bandwidth of the channel used to carry the data. In a SerDes the integration band generally matches the region outside the bandwidth of the clock and data recovery (CDR) used to sample the received data.
5. Presentation of Jitter
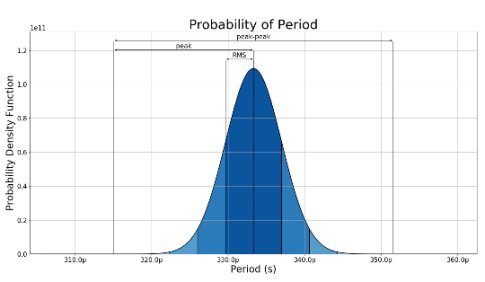
Figure 5: Example Probability Distribution for Random Jitter
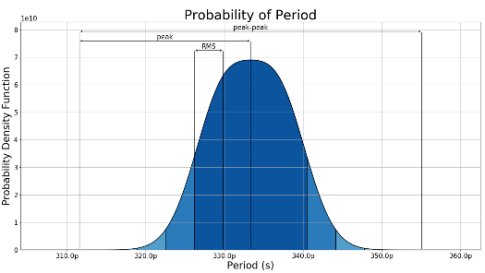
Figure 6: Example Probability Distribution for a combination of Random and Deterministic Jitter
Figure 5 and Figure 6 show the three ways that Jitter is usually quantified:
- Root Mean Square (RMS) jitter can be used to quantify or specify random jitter components. The RMS value can be considered equivalent to the standard deviation (σ) of a normal distribution.
- Peak-to-peak jitter is the difference between the longest and the shortest cycle. Peak-to-peak jitter can include both random and deterministic jitter components.
- Peak jitter is the difference between the shortest (or longest) cycle and the mean period of the clock. This is essentially half of the peak-to-peak jitter value.
RMS, peak and peak-to-peak can all be used to quantify any of the three types of jitter discussed in section 4: period jitter, cycle-to-cycle jitter and accumulated jitter.
5.1. Conversion Between RMS, Peak and Peak-Peak
Peak-to-peak jitter is twice the peak jitter, because in almost all cases the probability distribution is symmetric. In principle it is possible to have an asymmetric distribution, but this is so rare that it can be neglected.
Conversion between RMS jitter and peak jitter is more complicated because a normal distribution is unbounded, so in principle there is an infinitesimally small (but non-zero) chance of infinite instantaneous jitter on any sample. However, this is a theoretical limit and in practice, the bandwidth limited nature of PLLs and other clock sources mean that jitter tails will be truncated. In particular, because period jitter is measured across a single period, the bandwidth within which the period can be modified is very limited, so the real probability will be lower than calculated.
The designer of a system must choose the acceptable probability of jitter being above the peak jitter, i.e. the probability that a period will be outside the mean period +/- the peak jitter. From this, the ratio between peak and sigma can be determined.
The table below, gives the probabilities that a peak value will be exceeded for different multiples of the RMS value.
| RMS (σ) multiple | Probability of exceeding the peak | Application |
| 4 | 6.33 × 10-5 | Common multiple for digital system for period jitter (JESD65B) |
| 5 | 5.73 × 10-7 | Often used in high performance digital systems with critical performance requirements. This is the value specified on Perceptia Datasheets. |
| 7 | 2.56 × 10-12 | Commonly used multiple within SerDes specifications for accumulated jitter. Often specified as a bit error rate (BER) of 2.56 × 10-12 or 14σ peak-to-peak. |
6. About the Author
Julian Jenkins, is the CEO and CTO of Perceptia Devices. As CTO, he is the architect of all of Perceptia’s PLL IP where he been among the pioneers in the development of all digital PLLs. Julian has several US and international patents as a result of this work. He has participated in an impressive list of high-speed analog and mixed-signal ICs that are in commercial production. Feel free to contact Julian if you have questions about this topic.
Perceptia Devices is an IP and design services provider, based in Sydney, Australia and Silicon Valley. It is focused on PLLs for RF systems and demanding clocking applications.
